Atestat Info C++ – Albert Raspberry Pi 4B

Șuhan Nicoleta

prof. Erhan Mihail

Graf conex cu matrice de adiacență

Enunț :

În fișierul de intrare se află scrise pe prima linie două numere naturale n și m reprezentând numărul de noduri, respectiv numărul de muchii pentru un graf neorientat G=( X, U ). Pe următoarele m linii se află scrise extremitățile celor m muchii. Se cere să se construiască şi să se afişeze matricea de adiacență a grafului, precum și să se afișeze dacă graful introdus este conex sau nu.

Definiție: Un graf neorientat se numește graf conex dacă pentru oricare două noduri x și y diferite ale sale, există cel puțin un lanț care le leagă, adică x este extremitatea inițială și y este extremitatea finală.

Observație: Un graf cu un singur nod este, prin definiție, conex.

Definiție: Se numește lanț o succesiune de noduri L={x1, x2, x3, … , xk} cu proprietatea că oricare două noduri consecutive sunt adiacente.

Exemple:

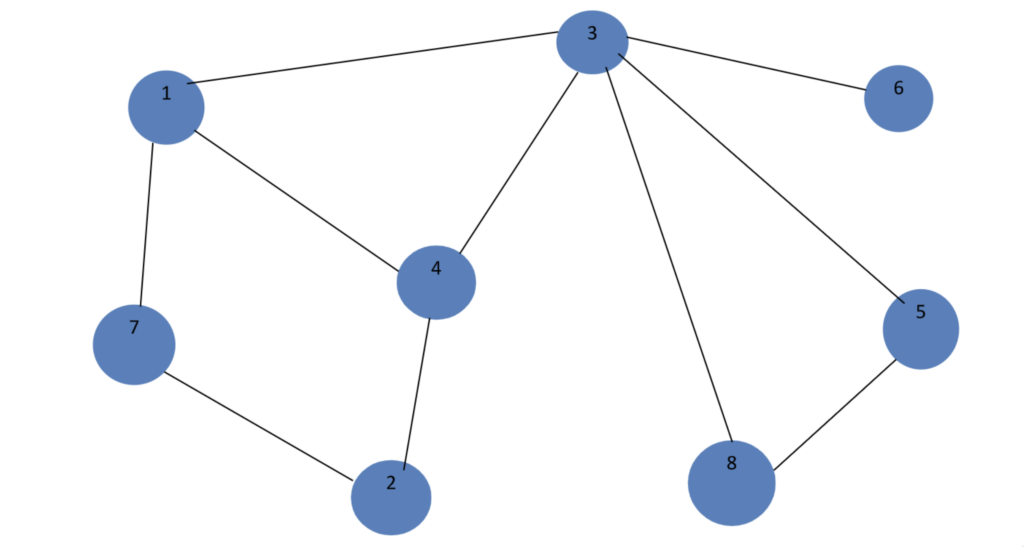
Pentru primul graf vom adăuga datele de intrare în fișierul conex.in , pe prima linie vom introduce, în această ordine, numărul de noduri și numărul de muchii ale grafului urmând ca pe următoarele linii să introducem toate extremitățile muchiilor existente.

Conținutul conex.in	Rezultate așteptate
8 10 1 3 1 4 1 7 2 4 2 7 3 4 3 5 3 6 3 8 5 8	Matricea de adiacenta este: 0 0 1 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 Graful este conex Elementele conexe sunt 1 1 2 3 4 5 6 7 8

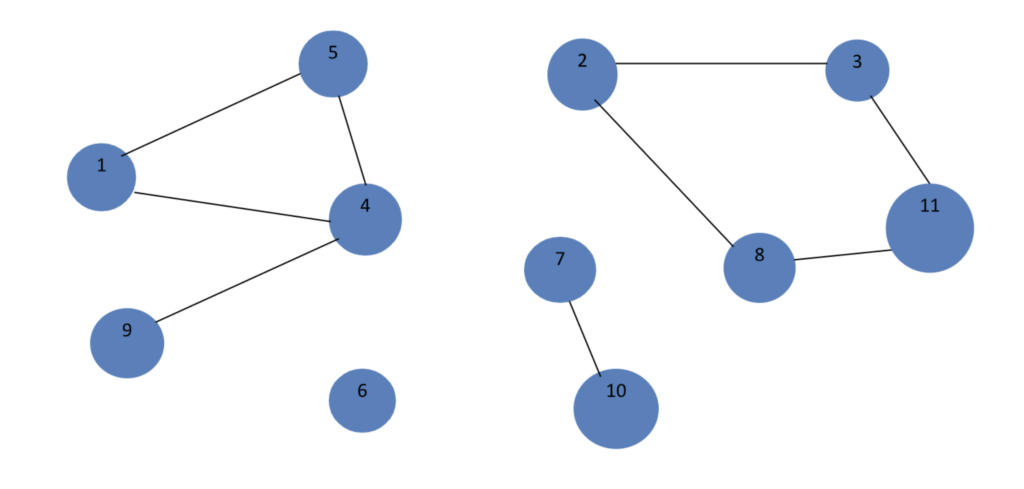
Atunci când graful introdus este neconex datele de intrare vor fi adăugate în fișierul neconex.in, algoritmul funcționând la fel.

Continut neconex.in	Rezultate așteptate
11 9 1 4 1 5 4 5 4 9 2 3 2 8 3 11 8 11 7 10	Matricea de adiacenta este: 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 Graful nu este conex Elementele conexe sunt 4 1 4 5 9 2 3 8 11 6 7 10

Următorul cod reprezintă problema rezolvată integral, urmând ca fiecare secvență să fie explicată:

#include <iostream>
#include <fstream>
#define dimensiune 100
 using namespace std;
 void citire(int &n, int &m, int a[][dimensiune])
{
    int e1,e2;
    ifstream in("conex.in");
    in>>n>>m;
    for(int i=1; i<=m; i++)
    {
        in>>e1>>e2;
        a[e1][e2]=1;
        a[e2][e1]=1;
    }
    in.close();
}
 
void afisare(int n, int a[][dimensiune])
{
    cout<<"Matricea de adiacenta este:"<<endl;
    for (int i = 1; i <= n; i++)
        {
                for (int j = 1; j <=n; j++)
            {
                cout<<a[i][j]<<" ";
            }
            cout<<endl;
        }
}
 
void afisare_elemente_conexe(int n, int culoare, int viz[])
{
    cout<<endl<<"Elementele conexe sunt "<<culoare-1<<endl;
    int ok = 0;
    for (int c = 0; c <= culoare; c++)
    {
        for(int i = 1; i <= n; i++)
            if(viz[i] == c)
            {
                cout<<i<<" ";
                ok = 1;
            }
        if(ok == 1) cout<<endl;
        ok = 0;
    }
}
 
int legatura(int a[][dimensiune], int x, int y)
{
    return (a[x][y] == 1);
}
 
void BFS(int a[][dimensiune], int n, int viz[], int coada[], int ns, int c)
{
    int i;
    coada[1]=ns;
    viz[ns]=c;
    int pi=1;
    int ps=1;
    while(pi<=ps)
    {
        for(i=1;i<=n;i++)
            if(viz[i]==0 and legatura(a, coada[pi], i))
            {
                coada[++ps]=i;
                viz[i]=c;
            }
            pi +=+ 1;
    }
}
 
 int main()
{
    int c=0,i,n,m;
    int a[dimensiune][dimensiune];
    int viz[dimensiune] = {0}, coada[dimensiune] = {0};
    citire(n,m,a);
    afisare(n,a);
    for(i=0;i<=n;i++)
    {
        if(viz[i]==0)
        {
            c++;
            BFS(a,n,viz,coada,i,c);
        }
    }
    if(c==2) cout<<"Graful este conex";
    else cout<<"Graful nu este conex";
    afisare_elemente_conexe(n,c,viz);
}

Secvența 1 : Funcția ”citire”

void citire(int &n, int &m, int a[][dimensiune])
{
    int e1,e2;
    ifstream in("conex.in");
    in>>n>>m;
    for(int i=1; i<=m; i++)
    {
        in>>e1>>e2;
        a[e1][e2]=1;
        a[e2][e1]=1;
    }
    in.close();
}

Aceasă funcție are rolul de a memora valorile lui n și m, adică, mai exact, numărul de noduri și numărul de muchii ale grafului. Pe lângă acești doi parametrii, funcția va primi ca parametru și o matrice de adiacență a[][dimensiune] care va memora valoarea 1 dacă există muchie de la nodul e1 la nodul e2, respectiv 0 în caz contrar.

Secvența 2 : Funcția ”afișare”

În funcția ”afișare” avem două secvențe repetitive cu determinare de tipul for, având rolul de a afișa matricea de adiacență de dimensiune [n][n] citită anterior corespunzătoare grafului dat.

void afisare(int n, int a[][dimensiune])
{
    cout<<"Matricea de adiacenta este:"<<endl;
    for (int i = 1; i <= n; i++)
        {
                for (int j = 1; j <=n; j++)
            {
                cout<<a[i][j]<<" ";
            }
            cout<<endl;
        }
}

Secvența 3 : Funcția ”legătură”

int legatura(int a[][dimensiune], int x, int y)
{
    return (a[x][y] == 1);
}

Funcția ”legătură” primește ca parametru matricea de adiacență și două noduri x și y. Returnează 1 dacă există legătură de la nodul x la nodul y. În caz contrar, returnează 0.

Secvența 4 : Funcția “BFS”

Această funcție reprezintă tehnica de traversare a lățimii, graficul sau arborele este parcurs în funcție de lățime. Această tehnică folosește structura de date a cozii pentru a stoca vârfurile sau nodurile și, de asemenea, pentru a determina care vârf / nod ar trebui să fie preluat în continuare.

Breadth First Search traversează graficul verificând mai întâi nodul curent și apoi extinzându-l prin adăugarea succesorilor săi la nivelul următor. Procesul se repetă pentru toate nodurile din nivelul curent înainte de a trece la nivelul următor. Dacă soluția este găsită, căutarea se oprește.

Breadth First Search este completă pe un set finit de noduri și optimă dacă costul deplasării de la un nod la altul este constant.

void BFS(int a[][dimensiune], int n, int viz[], int coada[], int ns, int c)
{
    int i;
    coada[1]=ns;
    viz[ns]=c;
    int pi=1;
    int ps=1;
    while(pi&lt;=ps)
    {
        for(i=1;i&lt;=n;i++)
            if(viz[i]==0 and legatura(a, coada[pi], i))
            {
                coada[++ps]=i;
                viz[i]=c;
            }
            pi +=+ 1;
    }
}

Secvența 5 : Funcția “afișare_elemente_conexe”

void afisare_elemente_conexe(int n, int culoare, int viz[])
{
    cout<<endl<<"Elementele conexe sunt "<<culoare-1<<endl;
    int ok = 0;
    for (int c = 0; c <= culoare; c++)
    {
        for(int i = 1; i <= n; i++)
            if(viz[i] == c)
            {
                cout<<i<<" ";
                ok = 1;
            }
        if(ok == 1) cout<<endl;
        ok = 0;
    }
}

Această funcție ia fiecare culoare în parte și verifică în vectorul viz care nod corespunde cu culoarea respectivă, urmând a-l afișa.

Secvența 6 : Funcția “main”

În funcția “main” vom introduce variabilele și vom apela fiecare funcție pe rând astfel încât la final să obținem matricea de adiacență a grafului și răspunsul la întrebarea dacă graful nostru este conex sau nu.

int main()
{
    int c=0,i,n,m;
    int a[dimensiune][dimensiune];
    int viz[dimensiune] = {0}, coada[dimensiune] = {0};
    citire(n,m,a);
    afisare(n,a);
    for(i=0;i&lt;=n;i++)
    {
        if(viz[i]==0)
        {
            c++;
            BFS(a,n,viz,coada,i,c);
        }
    }
    if(c==2) cout&lt;&lt;"Graful este conex";
    else cout&lt;&lt;"Graful nu este conex";
   afisare_elemente_conexe(n,c,viz);
}

Avantajele utilizării acestei metode de rezolvare a enunțului:
– Programul marchează al cărei componente conexe este fiecare nod.
– Interogarea dacă există muchie de la nodul x la nodul y este foarte ușoară.

Dezavantajele aceleiași metode:
– Timpul de execuție e mai mare.
– Structura de date utilizează mai multă memorie ( n^2 )

Optimizarea codului:
– Executarea BFS o singură dată și pentru a vedea dacă graful este conex se caută în vectorul viz[] valori de 0 (noduri nevizitate). Dacă există, graful nu este conex. Dacă nu există, graful este conex.

Exemple de grafuri din viața de zi cu zi:

Practic, un graf este un mod de a reprezenta elementele unei mulțimi şi conexiunile dintre acestea, stabilite pe baza unei anumite relații.

Harta unui oraș

Nodurile sunt intersecții, iar o muchie dintre două noduri reprezintă faptul că există o stradă între cele două intersecții. Atunci când reprezentarea unei astfel de rețele de intersecții şi străzi este un graf conex înseamnă că există o serie de străzi care leagă oricare două intersecții ale rețelei respective.

O rețea de socializare

Nodurile sunt utilizatorii, iar o muchie reprezintă relația de prietenie dintre doi utilizatori. Atunci când într-o rețea cu un anumit număr de utilizatori există o relație de prietenie între oricare doi utilizatori, directă sau prin intermediul unui/unor prieteni comuni, înseamnă că reprezentarea acestei rețele este un graf conex.

Motivarea alegerii temei

Breadth First Search este unul dintre cei mai simpli algoritmi grafici, și nu numai. BFS este utilizat pentru a afla cel mai scurt drum dintre două noduri dintr-un graf, fiind utilizat de sistemele de navigație GPS. De asemenea, este foarte important și pentru motoarele de căutare (Google, Bing, DuckDuckGo, etc.) pentru indexarea paginilor web.

Am ales această temă pentru atestat pentru că informatica e una dintre pasiunile mele cele mai mari, dar si pentru că BFS mi se pare unul dintre cei mai importanți algoritmi pentru lumea în care trăim.

Webografie:

https://www.routech.ro/algoritmi-grafic-si-structuri-de-date-explicate-cu-exemple-java-si-c/

https://www.pbinfo.ro/articole/810/grafuri-neorientate

https://grafneorientat.weebly.com/matricea-de-adiacen539259.html

https://profs.info.uaic.ro/~vcosmin/pagini/resurse_pregatire/resurse/graf_definitii.pdf

Link ideone : https://ideone.com/ecXaev